Forms – Emotions – Functions – Preferences
(Information approach)
Abstract
What is the nature of forms which are used in aesthetic objects? How to estimate these forms quantitatively? What may be recommendations for optimal usage of different forms? To answer these questions, is the main goal of this paper.
The investigation is based on the recent version of the information theory, based on the so-called ‘principle of the information maximum'. Using the methodology of consequent deductive unfolding of the initial postulate (maximization of ‘mutual information' between the object and its environment), it occurred possible to come to two fundamental results:
- pyramid-like multi-level (hierarchical) structure of information processing, with different paradigms used at each level; at each level both ‘gestalt' images and differential features can work, involving three types of memory; hence, a set of kinds of art, genres, and directions with appropriate devices appears;
- three-phase perception (rejection, acceptance, and stagnation) when a subject meets any new object; each phase is characterized by quite definite devices to be used, in order to provide positive emotion of a recipient.
All the devices deduced, are illustrated with appropriate concrete examples of their application. However, beside various ‘partial' devices, there exists the need to achieve the harmonious structure of the object as a whole, the so-called ‘unity of variety'. Mathematical formalization of this requirement comes to definite optimal forms which are really met in various kinds of art, objects of design, etc.: proportion of the ‘golden section', consonances of the musical scale, and so forth. Moreover, when applying psychophysical Stevens' law to empirical data on preferences, it occurred possible to estimate the ‘weight' of information carried by forms, when perceiving objects. In some cases the subject's attitude is characterized by minimization of information carried by forms (pictures, posters). But in all the situations information approach gives recommendations for usage of optimal forms.
What is true about art is true about life.
In every sphere of life form is the beginning of things.
Oscar Wilde, The Aphorisms (1905)
Among theoretical categories, form is one of the oldest, especially when it is used in contrast with such categories as ‘substance', ‘content', and other matters (or ‘style against material' in the concept of Russian formalists). However, we shall not dwell upon the roots of this category: our task is to analyze the problem of form in the framework of quite new approach which appeared in humanitarian studies in the 1980-90's. It is based on the contemporary version of the information theory.
Earlier, various attempts were made to apply the information theory in studies of art and culture (see, e.g., Moles, 1958; Bense, 1969). But they were unsuccessful, mainly because of non-systematic character, arbitrariness of initial assumptions, etc. The new version of the information approach is devoid of such shortcomings; that is why it occurred applicable to rather broad circle of phenomena relating to psychology, sociology, economics, history, linguistics, art studies, etc. (see, e.g., Golitsyn, 1997; Golitsyn & Petrov, 1995). In the given paper, we present only some of the results dealing with perception of forms and related phenomena.
1. Contours of general model (devices used by art
The departure point of new approach is the concept of ‘mutual information' between the system and its environment, introduced by Robert Fano (1951). If we have two variables x and y (e.g., x describes the conditions of the environment, y being the states of the system studied), then mutual information between these two variables can be defined through the symmetrical expression:
I (x, y) = log2 [p(x, y) / p(x) p(y)],
where p(x), p(y) are probabilities of the values x and y; and p(x, y) is the joint probability of the combination of x and y.
The basis of the model is the ‘principle of the information maximum': the system aspires to choose such state y which provides maximum mutual information with conditions of the environment x. Appropriate formalization of this principle comes to the equation concerning the maximum of the function:
where H(Y) is the unconditional entropy of the system's behavior, H(Y / X) - its conditional entropy, R(X, Y) - the resource expense in the state (X, Y), and β is the deficit of resources. [If the deficit of the resource available R is absent, then β is equal to zero; if the system suffers from the lack of the resource, then β is equal to unity. The nature of the resource may be: substance or energy needed for functioning of the system, the number of operations needed to fulfill each given kind of activity, etc.] This equation is valid for systems of rather different nature: biological species, man, society, language, kind of art, etc.
Unfolding the above model, it occurs possible to come to ‘three whales' consisting the ‘basement' of the information theory of culture and art.
A. Information processing in any complex system (e.g., human being) takes place in a multi-level hierarchical structure (Fig. 1). Each M-th level of this structure receives information from its preceding, M-1-th level, processes this information, and transmits its most valuable part upwards, to the M+1-th level. As well each M-th level formulates certain criteria KM for its preceding M-1-th level, concerning choice of the most valuable information to be transmitted upwards. In such a structure, each M+1-th level is working with the data relating to more general properties of the environment, than M-th level (examples see below). So, within such a structure, the information is subdued to two types of transformations:
- processing at each given level, in the framework of a certain paradigm;
- transmittal to the higher level, with a change of working paradigm.
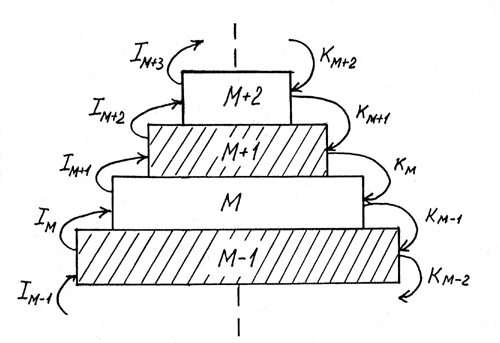
B. At each level of this hierarchical structure, two kinds of symbols can be used, relating to:
- concrete ‘gestalt' images, representing various real objects or phenomena (or sometimes unreal ones); at one level such images may be John, Peter, Mary, etc.; at another level such images may be a man, a woman, a boy, a girl, a baby, etc.; and we can find a higher level where such images are: a human, a tree, a dog, a wolf, etc.;
- rather abstract differential features relating to some properties that are common for different objects of the environment; at one level such features may be a color (white, red, green, etc.), dimensions of objects (their length and width), loudness, etc.; at another level such features may be: fitness for food, attribution to the organic or inorganic world, to the world of flora or fauna, etc.; and we can find a level where such features are a degree of human consciousness, humanistic attitudes, etc.
C. Functioning of the above hierarchy requires three principal steps of memory, which respond to three kinds of information activity within this system:
- to receive current information, it is desirable to have a ‘short-range memory', which is characterized by high speed (working in a diapason up to .5 sec), - but low capacity (its volume of the information kept is not more than 7-8 units);
- to process information at each given level (in order to formulate the criteria which exactly part of the information is the most valuable), a ‘long-range memory' is needed, capable of keeping a giant information, - though it is working slowly;
- to transmit information upwards, to the higher level, it is needed to use an ‘intermediate memory', with not so high speed (working in a diapason up to several seconds), but rather large volume of the information.
To support stable and reliable working of such a complicated set of informational procedures (inherent in any human being), some special efforts are needed. This task can be solved by fabricating special objects capable of ‘training' their recipients in working within such a structure. The main class of objects destined for such purposes, is nothing else but art. [Of course, some other objects are also capable of realizing such functions, and first of all objects of design, using appropriate forms of objects, though for them these functions are not main, but collateral.]
Considering these special objects, we should take into account two aspects.
The first aspect concerns the degree of complexity of such objects; each object may be based on:
- stressing perceptual properties of a separate image (or symbol);
- stressing perceptual properties of a combination of images (or symbols).
The second aspect is the nature of structural ordering; such objects may be:
- ordered in space, meaning spatial configuration of their elements;
- ordered in time, meaning temporary sequence of elements.
At last, each of such objects can use one of two main information channels (other channels cannot be effectively used in real practice for the above purposes):
- visual channel (using optical properties of objects);
- acoustic channel (using sound properties).
Hence, to fulfill the above ‘training', a work of art (or maybe certain practical object, which makes such a ‘training') should contain devices capable of realizing at least one of the above ‘modalities'. Their nomenclature is the combination of:
- two types of information processing (working within each level or transmittal of the information upwards);
- two kinds of symbols used (gestalt images or differential features);
- three steps of memory (short-range, long-range, and intermediate);
- two degrees of object complexity (stressing perceptual properties of separate objects or object combinations);
- two kinds of objects' ordering (in space or in time);
- two information channels used (visual or acoustic).
So, in total 2 ∙ 2 ∙ 3 ∙ 2 ∙ 2 ∙ 2 = 96 training modalities are potentially possible, to say nothing of their combinations probably realized in the same objects. Moreover, in addition to these specific (‘genuine') impacts, such objects can fulfill some other (collateral) functions, e.g., practical ones. [For instance, a work of prose may carry information about certain events; a picture may carry depiction of a certain landscape, and so on.] However, not all these modalities possess great vitality, mainly because of non-compatibility of some of their properties. Nevertheless, a giant number of devices - based on appropriate forms of special objects - is possible, materialized in various kinds of art, genres, directions, etc. Examples of such modalities are:
- training of processes within a given level of the hierarchy, operating with concrete images, combination of several images, using short-range memory, visual channel, and ordering in space, - is realized by some genres of figurative fine arts (still-life, interior, etc.), as well as by objects of architecture;
- the same kind of training, but using ordering in time, is realized by dance;
- almost the same kind of training, but using acoustic channel and ordering in space, is realized by most genres of poetry;
- the same kind but with ordering in time, responds to most genres of prose.
[Further genre concretization can be reached by taking into account concrete modes of each channel, e.g., black-and-white vision, color vision, accommodation, convergence of eye axes, etc. And if we aggregate some modalities in accordance with the information channel used, we come to traditional division of art into kinds.]
Now let us turn to those means by which these kinds of ‘mental training' can be realized: emotions which should accompany perception of such objects.
2. Model for general contours (art to use devices)
As far back as in 1960's, some concepts appeared connecting emotions with information. Pavel Simonov (1966) proposed a model connecting the emotion (E) while a certain activity, with the information (IN) needed for this activity, and real information available (IA): E = N (IA - IN), N being the coefficient reflecting the necessity of the appropriate information. So, if a person has enough information for his/her activity, his/her emotion will be positive, otherwise it will be negative. Nevertheless, this approach was not fruitful: firstly, the coefficient N itself depends on the values of IA and IN ; secondly, it is unknown how to determine these values.
From the systemic point of view, one can suppose that emotion is not an objective ‘goal in itself', but should be determined by the entire system of the human behavior. [For instance, we know that sexual pleasure is not the objective goal of a subject; the destination of this pleasure is to provide appropriate reproductive activity.] That is why Pyotr Anokhin (1978) proposed the concept of emotion as an indicator of the effectivity of activity: the higher the effectivity, the higher appropriate positive emotion. On the contrary, low effective activity results in negative emotion.
In the framework of the information approach, this concept looks as follows. At any level, it is necessary to have not only "global" goals of behavior, but also certain local indicators of approaching to the goal. [In mathematical terms, such an indicator is a partial derivative of the system's objective function over time.] Such an indicator is nothing else but the emotion: when approaching to the goal, emotion is becoming positive and rather high. For instance, when a prose-writer sees his new novel edited, his emotion is highly positive, because his activity occurred effective, and maybe he becomes closer to his goal, i.e. Nobel prize! [As well, some kinds of vandalism also occur very effective, e.g., setting fire.] On the contrary, moving away from the goal, results in negative emotion. For example, Sisyphus activity (to roll a stone upwards, this stone after that sliding downhill) generated his negative emotions, because of zero result of his efforts, and hence, their zero effectivity.
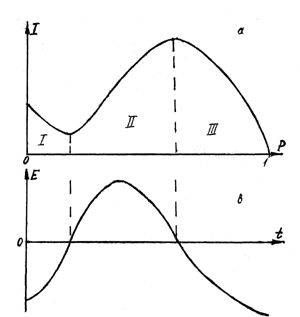
In the framework of this model, it occurred possible to obtain the dynamic regularity of emotion caused by any new stimulus (i.e. a new object perceived by a subject). This regularity deals with the ‘mutual information' between the object and the subject (I): it depends on the probability (p) to meet an object possessing exactly such properties as the given object. [While contact, this probability changes from zero to unity.] As it was shown theoretically, the dynamics of the ‘mutual information' passes through three stages (Fig. 2a):
|
Figure 2. Dynamics of reactions when perceiving new object: a) dependence of the information (I) on the probability (p) of the given combination of parameters; b) dependence of the emotion (E) on time (t) when perceiving the object. |
I. ATTENUATION. When p is close to zero, the information I decreases with the growth of p. As far as such decreasing contradicts the aim of the subject, it causes his/her negative attitude towards the stimulus (object). The subject attempts to reject such a stimulus. In this stage, only a physical interaction between the subject and the object exists; genuine informational interaction is still absent.
II. AMPLIFICATION. At a certain moment, the information I starts increasing. The attitude of the subject to the stimulus becomes positive. At this stage the subject aspires to attract and to assimilate the stimulus, and to amplify it. This is a stage of the informational interaction between the subject and the object.
III. DEPRESSION. In the third stage, information decreases, and the attitude of the subject to the stimulus becomes negative again. This stage can be also called "stagnation", "fatigue". The only means to break off this stage is to switch to any "other", "contrast" stimulus.
Simonov (1962) was the first who investigated these three stages systematically. He generalized a large amount of facts and defined these stages in the language of physiology as ‘initial or preventive inhibition', ‘activation or excitation', and ‘supermarginal inhibition'.
As soon as emotion is a derivative of the mutual information, its dynamics passes through the same three phases (see Fig. 2b):
I. REJECTION. In this stage the emotion is negative. The subject can simply "switch off" his attention and stop perceiving the stimulus. But if he/she can compel him/herself to go on perceiving, then sooner or later the next stage sets in.
II. ACCEPTANCE. The emotion becomes positive. In this stage, the subject aspires to prolong the perception, in order to continue receiving positive emotion.
III. STAGNATION. The emotion becomes negative again, the stimulus is ‘boring'. Hence, the subject aspires to switch to another stimulus. Then a new cycle of activity begins.
We can find these three stages in many processes of perception on different levels of organization. So the perception of any new idea, scientific concept, or new trend in art usually passes through these three stages. The optimal tactics of behavior concerning these three stages, consists of the following rules:
- To overcome the first stage as fast as possible.
- To prolong the second stage for as long as possible.
- To switch to ‘other', ‘contrast' stimulus at the beginning of the third stage.
There exist various concrete ways to realize the appropriate behavior of a subject when perceiving works of art and other objects realizing ‘training'.
Of course, to carry pleasure, is not the main function of works of art. However, it is impossible to do without mechanisms which provide pleasure received by a recipient. [Otherwise he/she would refuse to perceive the oeuvre.] That is why the optimization of emotions should be applied to each oeuvre (or each part of it).
The means organizing the perception of each oeuvre (or its part), connect elements of the oeuvre with each other, which can be realized by two ways:
- by full repetition of features;
- by partial repetition of features.
Let us compare these two classes (Golitsyn, 1997). Devices of both classes can be used at the first stage, in order to overcome the threshold of perception (i.e. to attract the recipient's attention to the oeuvre or its given segment). As well, both classes can be used at the second stage, for its prolongation, accompanied by positive emotions. However, it is profitable to use the full repetition during the first stage, and the partial repetition during the second stage. Why? - In psychology there exists the well known regularity: there are some features that are perceived and recognized at the first sight, more easily than others, and features which can keep attention for a longer time. Examples of these two classes are presented in the Table below.
It is a fact that the devices belonging to the left column, are perceived and recognized earlier than those ones of the right column. Really, we perceive contrast before nuance, identity before proportions, generalized forms before details, and so forth. That is why the devices of the left column are more adequate to overcome the first stage, and the devices of the right column - to prolong the second stage.
|
FULL REPETITION |
PARTIAL REPETITION |
Contrast |
Nuance (variation) |
|
Identity (refrain, leit-motif, reminiscence, comparison, allusion, imitation of reality, etc.) |
Similarity, proportion, architec--tural ‘module', transposition, conso-nance, elaboration of musical theme |
|
Generality |
Detail |
|
Continuity |
Discretion |
|
Straight line |
Curved line |
|
Smooth contour |
Broken contour |
|
Metre |
Rhythm, rhyme |
|
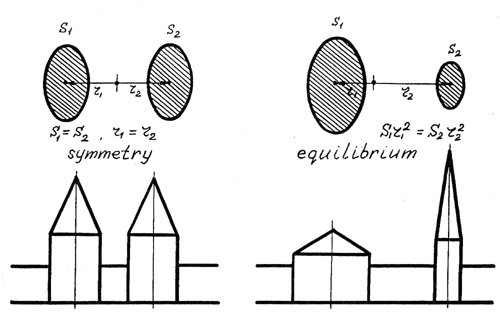
Symmetry |
Equilibrium |
Partial repetition (when only part of the features or their combinations are repeated) can be considered as a further development of the full (simple) one. So equilibrium in painting and architecture is a further development of simple symmetry. In this case, areas of volumes should not be equal, but combinations of them (as the product of the area to its distance from the centre, Fig. 3) should be.
Other examples of partial repetition are similarity and proportion in architecture, and transposition in music. In this case, the combination repeated is a relation of features (lengths, frequencies, etc.), but not features themselves (Fig. 4). These devices can be considered as a development of identity when the features themselves are repeated.
Many geometrical and topological transformations change one part of the figure's features and preserve other features or their combinations (‘invariants'). For instance, a curve remains a straight line, circle, parabola, etc., and only its parameters (inclination, radius, crookedness, etc.) vary. Folds in clothes, lines of waves, rays of light, and other examples show us transformations and their invariants in ornament, design, graphic arts, and so on.
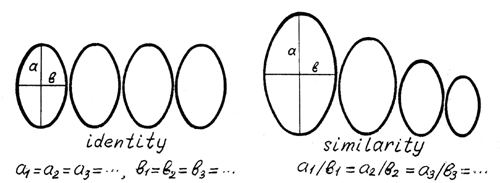
Figure 4. Examples of identity and similarity.
In poetry we find such examples of partial repetition as rhythm (coincidence of a part of the accents) and rhyme (coincidence of a part of phonemes). It is important to emphasize the word ‘part': lack of coincidence destroys rhythm and rhyme, full coincidence impoverishes them.
In music we find such examples of partial repetition as consonance - coincidence of a part of overtones; transposition - when absolute altitudes of sounds change, but intervals between them are preserved; variation and elaboration of musical theme, etc.
In architecture and music we find such a device as a module, based on partial repetition. A module is a common unit of length or longitude for spatial or temporal segments, used in a work of art. Lengths or longitudes of these segments should be divisible - without remainder - by this unit. It allows variety and, at the same time, provides a unity of spatial or temporal relations in the work of art (or any other object). The time (or part of it) is the example of a module in music. It provides the unity of metrical and rhythmical correlations in music. The step of division is an example of a module in architecture.
An example of combining devices of the first stage and the second one, is a musical device like the ‘vibrato' - slight oscillation of force, frequency, or other parameters of sound. The typical picture of the development of sound is shown in Fig. 5. The sound begins as ‘straight' and even (simple repetition), because it takes some time for a new sound to overcome the threshold, to be perceived and identified by the listener. But soon such simple continuation becomes ‘boring', uninformative. Slight deviations of parameters of sound arise, the amplitude of these deviations increases, and at last the sound is replaced by another sound. Then the picture is repeated.
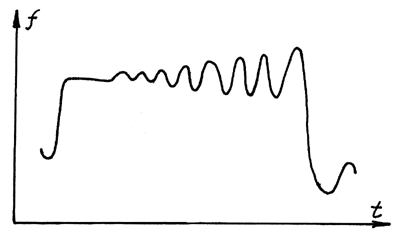
Figure 5. Vibrato: dynamics of force (f), or frequency, or other parameters of sound.
But sooner or later partial repetition and nuance variations of the stimulus exhaust their possibilities for maintaining informativeness of the stimulus and keeping the attention of the subject. Then a more radical change becomes inevitable: the subject abandons the old stimulus and begins to search for any essentially new, ‘other' stimulus. And he should find this stimulus in the framework of the work of art - otherwise he will find it somewhere else, he will turn away from the object.
It is the third stage of the interaction between the subject and the object. The artist (painter, designer, writer, etc.) should provide the subject with an opportunity for such searching by a special organization of the object perceived. The main means for this is contrast. For instance, in the structure of the oeuvre each element (‘stimulus') "must be accompanied (in time or space) by another, contrast stimulus. In temporal arts (theatre, literature, music) the artist himself must alternate one stimulus with another one: tragic with comic, loud with silent, slow with quick, etc. In spatial arts (painting, architecture), he must give the spectator the opportunity to alternate this stimulus with the other contrasting one: dark with light, great with small, high with low, and so forth" (Golitsyn & Petrov, 1995, p. 157-158). Such are the ways to ‘switch' recipient's attention to another object.
As well, for us it is time to switch the reader's attention to the emotions accompanying perception of an object as the totality.
3. Preferences of forms and forms of preferences
These ‘resulting' emotions are formed on the basis of the processes at all levels of our structure (though with different ‘weights'), caused by different devices. Of course, in many cases negative emotions dominate the perception; these cases are:
- monotony, when the variety (entropy) inherent in the oeuvre (or any other object) is less than the variety of recipient's reactions [H(X) < H(Y)]; subjectively such a situation is nothing else than ‘boredom'; it is the third stage of perception;
- tensity, when the variety of the oeuvre exceeds the variety of recipient's reactions [H(X) > H(Y)]; subject feels ‘lack of harmony', ‘fussiness', ‘fatiguing noise', etc.; stimuli of the first stage of perception are dominating;
- lack of agreement between impulses from the object and a store of recipient's reactions; here both monotony and tensity are present, and the subject feels ‘incomprehensibility', ‘strangeness', ‘bizarrerie', etc.
However, a certain ‘fortunate' situation is possible, when the resulting emotion is positive. Usually we meet such situations when a large amount of devices are united for the achievement of one goal: harmony of a whole. This harmony is the totality of some relations (spatial, temporal, logical, numerical, etc.) between the features of an object. Maybe the most famous one is the ‘golden section' which was already known in ancient times; the others are musical series constants (see also Golitsyn, 1997).
The main idea of the harmonic organization of an object is the so-called ‘unity of variety'. Let us consider any two elements (spots, lines, sounds, etc.) of an object. Each of them can be described by means of some features (color, length, frequency, etc.). Let us call these features x for the first element and y for the second one. Then the variety of the variable y is expressed by the entropy H(Y), the unity between y and x - by the conditional entropy H(Y/X) (with the sign minus), and the unity of variety can be described by means of mutual information between these variables:
I (X,Y) = H(Y) - H(Y/X).
According to the principle of the information maximum, the organization of an oeuvre is intended to achieve the maximum of this quantity. The more H(Y), the more self-information (variety) variable y contains. The less H(Y/X), the more the order and organization of the oeuvre, the easier to predict y if we know x.
But we remember that it is also necessary to take into account the economy of resources R(X,Y), so that a third item should be supplied to the expression (3):
L(X,Y) = H(Y) - H(Y/X) - β R(X,Y) → max.
So, in accordance with this expression [quite analogous to (2)], the general principle of harmonic organization of the object is ‘unity, variety, and economy'.
A propos, three items in equation (4) respond to three main types of associations which determine the movement of recipient's attention, and naturally they unite the elements perceived in a certain totality: associations by contiguity (minimal resource expense R(X,Y) when transition from x to y), associations by likeness (minimum H(Y/X)), and by contrast (maximum H(Y)).
Let us consider two concrete models resulting in the phenomenon of ‘golden section' and numerous related phenomena. Both models deal with comparison of two elements (linear segments, areas of spots, frequencies of musical sounds, etc.).
The first model proceeds from the assumption that the resource R is proportional to the number m of operations, R = am, which is necessary to determine a relation of two quantities x0/x1. For clearness, we shall look at a relation of two linear segments (Fig. 6). The process looks as follows: we compare segments, subtracting the lesser segment x1 from the greater one x0. If the number of subtractions is exactly m1 , the problem is solved and the relation x0/x1 = m1 . If there is some remainder x2, such that x0 = m1 x1 + x2, we should evaluate the size of the remainder. We can do this by repeating the same procedure, i.e., subtracting the remainder x2 from the lesser segment x1. The procedure should be repeated until the last remainder xn+1` becomes less than the setting error of measuring. Then the last segment xn can be treated as module μ - the common unity of measurement of two segments. As it was shown, if the subject possesses the total resource of m operations, then the total amount of information I, received in measurements, is equal:
I = m log (m + 1).
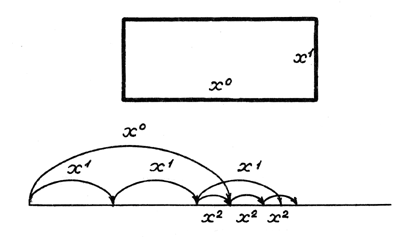
If we exchange the scale of x so that the module (‘natural unit of measurement') would be equal to one: xn-1 = xn = μ = 1, then we obtain the sequence of segments x0, x1, ..., xn which provides receiving maximal information. This sequence is nothing else than the well known Fibonacci series taken in the inverse order: 1, 1, 2, 3, 5, 8, 13, 21, 34, ... One of the most important properties of this series is that if the number of operations is rather large, the relation of two consequent items of the series is equal to the ‘golden section':
lim xk / xk-1 = 1.618...
k → ∞
Hence, if resource R is unlimited then m can be infinite and the relation xk/xk-1 can be equal to the golden section 1.618... Otherwise (total m is constrained), xk/xk-1 has to be one of the relations of the Fibonacci series. It is not occasionally that the simplest of these relations correspond to the consonances of the musical scale:
1 / 1 = tonic; 2 / 1 = octave; 3 / 2 = fifth, 5 / 3 = large sixth; 8 / 5 = little sixth.
The other consonances can be obtained as the inversion of these ones, i.e., as a ‘complement to the octave'. Mathematically, it is expressed as the division of 2 (= octave) by these relations:
4 / 3 = fourth = inversion of fifth = 2 : 3 / 2;
6 / 5 = little thirth = inversion of large sixth = 2 : 5 / 3;
5 / 4 = large thirth = inversion of little sixth = 2 : 8 / 5.
We should emphasize that not all the simplest rational numerical relations are able to be consonances, but only the members of the Fibonacci series and their inversions! For instance, number 7 is not a member of the Fibonacci series and such simple numerical relations containing 7, as 7 / 5 or 10 / 7 (diminished fifth and its inversion) are terrible dissonances! Maybe it is the solution of the old damned ‘problem of seven', that caused such pain to theorists of musical harmony?
This model allows us also to explain the following fact: we meet the golden section only in ‘static' arts, such as painting, architecture, sculpture, but not in music. Maybe the reason for this is that in static arts the time of perception (and, consequently, the total number of operations m), is practically unlimited and we can arrive at the absolute maximum, which is the golden section. But in music, where the time of perception is limited in principle, we have to be satisfied with the conditional maximum, which gives us only the simple relations of the Fibonacci series.
|
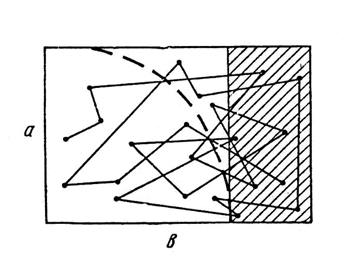
Figure 7. Comparison of a rectangle's sides. |
Concrete realization of such measurement may be based on the process of visual perception consisting in the synthesis of signals, received from a number of discrete ‘points of fixation'. These points respond to positions of the pupil of the eye when it stops on different places of an object perceived. The movement of the pupil between these points is chaotic; it depends on many circumstances, and first of all on the ‘content' of the object. As far as now we consider quite ‘empty' objects (i.e., simply rectangles), the points of fixation are to be distributed homogeneously over the surface of the object: the pupil is simply ‘scanning' this surface, with equal probability to be fixed at each point. [Here we neglect the ‘edge effect': we assume that the number of the ‘points of fixation' relating to the rectangle, is many times more than the number of such points needed to feel the border of the object.] So in order to measure the form, a subject can compare the number of signals from ‘points of fixation' relating to ‘unbalanced' part of the rectangle, and to its square part.
So, if the probability of the point of fixation to respond to the ‘unbalanced' part or to the square one is p1 or p2, respectively (of course, p1 + p2 = 1), then the information I received by a recipient, is determined by C.Shannon's formula:
I = - p1 log2 p1 - p2 log2 p2 .
However, when analyzing the signals, only those of them are singled out which come from the ‘unbalanced' part, and we can assume that
I = - p1 log2 p1 .
As soon as the number of signals from each part is proportional to its area,
p1 = (b - a) a / ab = 1 - x ,
x = a / b being the ratio of the rectangle's sides, or its proportion. Therefore, the equation (8) will become:
I = (x - 1) log2 (1 - x).
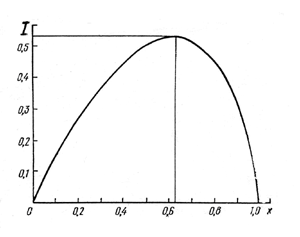
|
Figure 8. Information I (bits) carried by rectangular forms with proportions x. |
Now we should take into account that in our case an attitude toward maximal information predominates, so the more the information carried by the form, the higher the estimation of the form by subjects. This means nothing else than the maximal subject's estimation responding to the form with the ratio equal to .632. But this value is rather close to the one for the golden section: b/a = 1/1.618 = .618. [The difference of the amount of information carried by these two proportions (see Fig. 8), is quite negligible - about .1%.] Such a coincidence evidences in favor of the model used. So now it is clear why the form of the golden section is preferred in many cases.
Moreover, we can add another argument, dealing not with the maximum of the curve considered, but with the entire distribution (i.e., form) of subject's preferences.
As far as the information is a ‘substance' influencing upon a subject while perceiving forms, we can treat this ‘substance' as a stimulus and resort to the help of psychophysical regularities. Evidently, the probability to prefer the object which is a carrier of this stimulus (out of all other objects), plays ‘reaction' to such a stimulus. Hence, the connection between the quantity of the information I carried by such form, and the probability PA that this form is preferred, should be subdued to the well known psychophysical regularity, exactly Stevens' law:
PA = C Iγ ,
C and γ being constants characterizing each subject and kind of stimuli, respectively. In logarithmic co-ordinates on both scales, this dependence looks as linear.
The data to prove this regularity for forms, can be borrowed from different sources. G.T.Fechner (1876) was the first who investigated such preferences: he studied 347 subjects, each of them being proposed 10 rectangles of different proportions. Each subject was asked to indicate:
- the most attractive form; so the attractiveness (NA) of each form was determined as a number of subjects which preferred it; as well the probability PA to choose the given form was also determined;
- the most unattractive form; so the unattractiveness (NU , PU) was calculated.
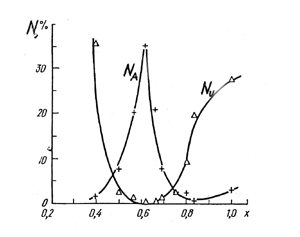
Fig. 9 presents both kinds of reactions in dependence of the proportion x. Naturally, the curve for the attractiveness NA has its maximum at the golden section, while the curve for the unattractiveness NU possesses its minimum at the same proportion. However, what is much more interesting, both dependences being built in logarithmic co-ordinates, occurred linear (Fig. 10), with the slope γ equal to 16.0 and 25.2 for attractiveness and unattractiveness, respectively (with standard deviation about .04 and .02). The coefficients of linear correlation were .90 and .97 respectively, both values being statistically significant at the level better than 1%.
|

|
|
Figure 9. Attractiveness (NA, %) and unattractiveness (NU, %) of rectangles with different proportions x. |
Figure 10. Attractiveness (PA) and unattractiveness (PU) of rectangles vs information (I) carried by their forms: logarithmic co-ordinates. |

Both absolute values of the coefficient γ, i.e., for the attractiveness and unattractiveness, are close to each other; evidently, mechanisms are common for both reactions. But the most important are very high values of γ : they are indicative of rather high significance of the information for subjects. For all other kinds of stimuli this coefficient varies from .33 (brightness of the light) to 3.5 (electric current). So the ‘weight' of the information contained in objects' forms, is many times more than ones for other kinds of stimuli! These results were completed by the contemporary data, in particular those ones obtained by Berlyne (1970). Again Stevens' law was fulfilled, though with slightly less values of the coefficient γ (Petrov, 1996).
* * *
In total, the attractivity of the golden section is supported by several many-sided arguments, though some researchers do not agree with this concept (Hoege, 1995), but some support it (Konecni, 1997). Maybe, this discrepancy is rooted in different attitudes of recipients involved in experiments, as well as objects investigated. Moreover, in some situations quite different attitudes are inherent in perception of different classes of objects. For instance, pictures require minimal information carried by their ‘outer' forms, so their preferred proportions should be far from the golden section. Posters are characterized by an ‘intermediate' type of their perception, so the distribution of their proportions is intermediate between those ones for ‘simple' objects and pictures (Petrov, 1996). But in all situations information approach gives recommendations for appropriate usage of optimal forms.
References
Anokhin, P.K. (1978). Beitrage zur allgemeinen Theorie des funktionalen Systems. Jena: Fischer.
Bense, M. (1969). Einfuerung in die informationstheoretische Aesthetik. Grundlegung und Anwendung in der Texttheorie. Hamburg: Rohwolts Deutsche Enzyklopaedie.
Berlyne, D.E. (1970). The golden section and hedonic judgements of rectangles: a cross-cultural study. Scientific Aesthetics, vol. 7, No. 1 / 2. P. 1 - 6.
Fano, R. (1951). Transmission of Information. NY; London: M.I.T.Press & Wiley.
Fechner, G.T. (1978). Vorschule der Aesthetik. Leipzig: Breitkopf & Haertel.
Golitsyn, G.A. (1997). Information and Creation: On the Road to Integral Culture. Moscow: Russky Mir (in Russian).
Golitsyn, G.A., & Petrov, V.M. (1995). Information and Creation: Integrating the "Two Cultures". Basel; Boston; Berlin: Birkhauser Verlag.
Hoege, H. (1995). Fechner's experimental aesthetics and the golden section hypothesis today. Empirical Studies of the Arts, vol. 13, No. 2. P. 131 - 148.
Konecni, V.J. The vase on the mantelpiece: The golden section in context. Empirical Studies of the Arts, vol. 15, No. 2. P. 177 - 207.
Moles, A. (1958). Theorie de l'information et perception estetique. Paris: Flammarion editeur.
Petrov, V.M. (1996). Golden section in the light of an informational approach. Rivista di Psicologia dell'Arte, Anno XVII, No. 7. P. 18 - 32.
Simonov, P.V. (1962). Three Phases of Reactions of Organism on Increasing Stimulus. Moscow: Nauka (in Russian).
Simonov, P.V. (1966). What is Emotion? Moscow: Nauka (in Russian).